Introducción
El aprendizaje por refuerzo es un área interdisciplinaria del aprendizaje automático que ha ganado popularidad en la última década debido a sus recientes logros en juegos como Ve y aplicaciones del mundo real como coches autónomos. Este crecimiento también ha coincidido con los rápidos avances de las GPU modernas y la evolución de las técnicas de aprendizaje automático. Hemos llegado a una etapa en la que las máquinas pueden superar fácilmente a los humanos en los juegos de ordenador. Deep Q-Network (DQN) es un nuevo algoritmo de aprendizaje por refuerzo que es muy prometedor para el manejo de videojuegos como Atari, debido a su gran dimensionalidad y a la necesidad de una planificación a largo plazo. En este tutorial se explicará cómo funciona el DQN y se demostrará su eficacia a la hora de derrotar al Lunar Lander de Gymnasium, anteriormente gestionado por OpenAI.
¿Qué es el aprendizaje por refuerzo?
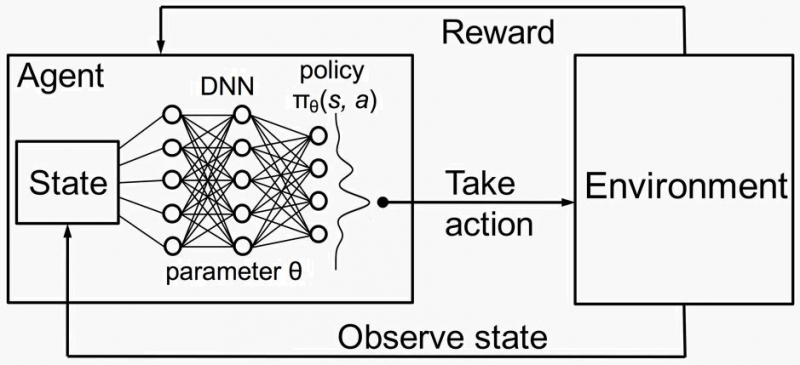
El aprendizaje por refuerzo implica que un agente tome decisiones realizando acciones en un entorno para maximizar las recompensas acumuladas. Los componentes clave de RL incluyen:
- Agente: El responsable de la toma de decisiones que interactúa con el entorno.
- Medio ambiente: el sistema externo con el que interactúa el agente.
- Estado (S): La situación o configuración actual del entorno.
- Acción (A): Los posibles movimientos o decisiones que puede tomar el agente.
- Recompensa (R): comentarios del entorno que indican la calidad de una acción.
- Política (π): una estrategia que mapea los estados con las acciones que definen el comportamiento del agente.
- Función de valor (V): Calcula la recompensa acumulada esperada de un estado determinado.
- Función Q (Q): Calcula la recompensa acumulada esperada por realizar una acción concreta en un estado determinado.
Cómo funciona el aprendizaje por refuerzo
- Inicialización: El agente comienza con un conocimiento mínimo o nulo sobre el entorno.
- Interacción: El agente interactúa con el entorno tomando medidas basadas en su política.
- Retroalimentación: El entorno responde a cada acción con un nuevo estado y una recompensa.
- Aprendizaje: El agente actualiza su política y/o funciones de valor en función de las recompensas recibidas para mejorar las decisiones futuras.
Conceptos clave
- Exploración frente a explotación: Equilibrar la exploración de nuevas acciones y la explotación de las acciones conocidas de alta recompensa.
- Factor de descuento (γ): Determina la importancia de las recompensas futuras en relación con las recompensas inmediatas.
- Ecuación de Bellman: describe la relación entre el valor de un estado y los valores de sus estados sucesores.
La ecuación de Bellman
La ecuación de Bellman es fundamental en el aprendizaje por refuerzo, ya que proporciona una descomposición recursiva de la función de valor. Relaciona el valor de un estado con los valores de los estados subsiguientes. La ecuación de Bellman para la función Q viene dada por:
$$ {{Q (s, a) =r+γ\ max_ {a'} Q (s', a')} $$
Aquí:
- $ {{Q (s, a)}} $ es el valor Q para realizar la acción aaa en el estado sss.
- $ {{r}} $ es la recompensa recibida tras realizar la acción aaa.
- $ {{\ gamma}} $ es el factor de descuento que determina la importancia de las recompensas futuras.
- $ {{\ max_ {a'} Q (s', a')}} $ es el valor Q máximo para el siguiente estado $ {{s'}} $ entre todas las acciones posibles $ {{a'}} $.
Aprendizaje por diferencia temporal
El aprendizaje por diferencia temporal (TD) es un enfoque clave en RL, que combina ideas de la programación dinámica y los métodos de Monte Carlo. Actualiza las funciones de valor en función de la diferencia (o diferencia temporal) entre el valor previsto y la recompensa real recibida, más el valor descontado del siguiente estado.
La regla de actualización para Q-learning, un tipo de aprendizaje de TD, es:
$$ {{Q (s, a)\ flecha izquierda Q (s, a) +\ alpha\ left (r +\ gamma\ max_ {a'} Q (s', a') - Q (s, a)\ right)}} $$
Aquí:
- $ {{\ alpha}} $ es la tasa de aprendizaje, que controla el grado en que la información nueva prevalece sobre la anterior.
- $ {{r+γ\ max_ {a'} Q (s', a')}} $ es el objetivo para el valor Q actual, que combina la recompensa inmediata y las recompensas futuras estimadas.

El aprendizaje por refuerzo es un marco sólido para resolver problemas complejos de toma de decisiones. Este marco aprende la estrategia óptima a través de interacciones de prueba y error con el entorno.
Cómo funciona DQN:
Deep Q-Network (DQN) combina el aprendizaje automático con redes neuronales profundas para gestionar entornos con numerosos estados y acciones.
Aprender de la experiencia
Q-learning es un algoritmo de aprendizaje por refuerzo en el que un agente aprende a maximizar las recompensas mediante interacciones con el entorno. Utiliza la función Q (s, a) para predecir las recompensas futuras. El agente actualiza los valores Q mediante la ecuación de Bellman y ajusta sus predicciones en función de las recompensas recibidas y las recompensas futuras esperadas.
Ejemplo práctico
Imagina estar en el estado sss con una Q (s, a) = 100 pronosticada. Tras realizar la acción a, pasáis al estado s' y recibiréis una recompensa de 8. El valor Q de la mejor acción en s' es 95, con un factor de descuento de 0,99. La diferencia temporal es $ {{8 + 0.99\ times 95 - 100 = 2.05}} $. Con una tasa de aprendizaje de 0,1, el valor Q actualizado pasa a ser $ {{100 + 0.1\ times 2.05 = 100.205}} $.
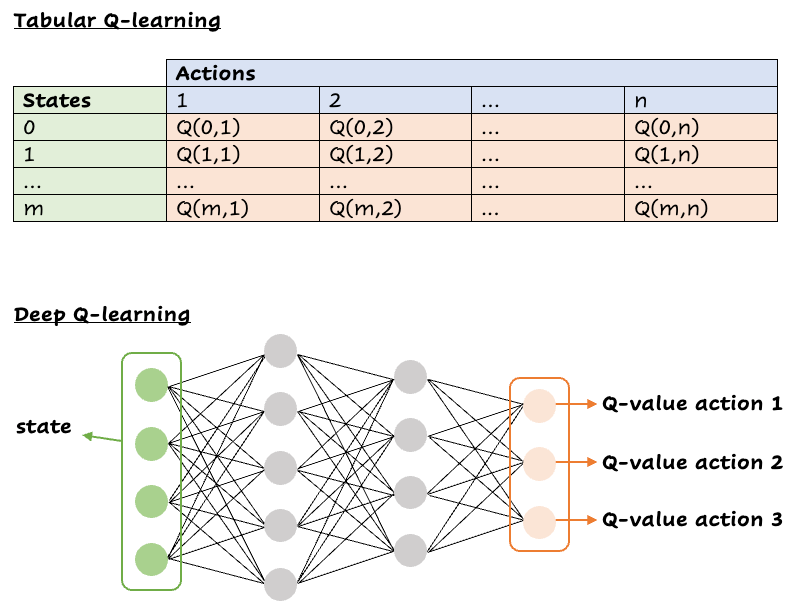
Q-Learning profundo
El aprendizaje Q tradicional utiliza una tabla para almacenar los valores Q, lo que no es factible en entornos con muchos estados y acciones. El DQN utiliza una red neuronal para aproximar Q (s, a), lo que permite al agente generalizar pares estado-acción invisibles. La entrada a la red neuronal es una observación y la salida es un valor Q para cada acción posible.
Algoritmo DQN
- Repetición de experiencias: almacena las experiencias (s, a, r, s') en un búfer de reproducción. El muestreo aleatorio del búfer ayuda a romper las correlaciones temporales, lo que hace que el aprendizaje sea más estable.
- Red objetivo: Utiliza dos redes neuronales: la red principal para la toma de decisiones y la red objetivo para proporcionar objetivos de valor Q estables.
- Pasos de entrenamiento:
Inicialice el búfer de reproducción y las redes.
Para cada episodio:
Inicialice el estado inicial.
Para cada paso:
- Selecciona la acción aaa usando una política codiciosa de\ epsilon.
- Ejecuta la acción y observa la recompensa r y el siguiente estado s'.
- Almacene la experiencia en el búfer de reproducción.
- Muestra un minilote del búfer de reproducción.
- Calcule el valor Q objetivo y realice un descenso de gradiente en la pérdida.
- Actualice la red de destino periódicamente.
Mejoras para la estabilidad
Para garantizar la estabilidad y la convergencia, se implementan varias mejoras:
- Selección de acciones de e-Greedy: Equilibra la exploración y la explotación ajustando la tasa de exploración a lo largo del tiempo.
- Repetición de experiencias: Permite aprender de lotes de experiencias pasadas, lo que garantiza una formación estable y una mejor convergencia.
- Red objetivo frente a red local: Utiliza una red de objetivos para proporcionar objetivos de valor Q estables, lo que reduce las oscilaciones y la divergencia.
Red objetivo frente a red local
En DQN, se utilizan dos redes para estabilizar el aprendizaje:
- Red principal (local): Esta red se actualiza continuamente y se utiliza para seleccionar acciones durante la formación. Aprende minimizando la pérdida entre los valores Q pronosticados y los valores Q objetivo.
- Red objetivo: Esta red proporciona objetivos estables para las actualizaciones del valor Q. A diferencia de la red principal, los pesos de la red de destino se actualizan con menos frecuencia, por lo general copiando los pesos de la red principal cada pocos miles de pasos.
¿Por qué usar dos redes?
- Estabilidad: Los pesos de la red principal se actualizan con frecuencia, lo que puede provocar inestabilidad y divergencia. Al utilizar la red objetivo para proporcionar objetivos de valor Q estables, evitamos oscilaciones rápidas en el aprendizaje.
- Coherencia: La red objetivo ayuda a mantener objetivos de aprendizaje consistentes, ya que solo se actualiza periódicamente. Esto garantiza que las actualizaciones del valor Q se basen en objetivos más estables y confiables, lo que conduce a un aprendizaje más fluido y estable.
Mecanismo de actualización
- Actualización de la red principal: Después de cada acción, la red principal actualiza sus ponderaciones utilizando la pérdida calculada a partir de la diferencia entre los valores Q pronosticados y los valores Q objetivo proporcionados por la red objetivo.
- Actualización de la red de destino: Cada pocos miles de pasos, los pesos de la red principal se copian a la red de destino, lo que garantiza que la red de destino proporcione objetivos estables para un número determinado de pasos antes de volver a actualizarse.
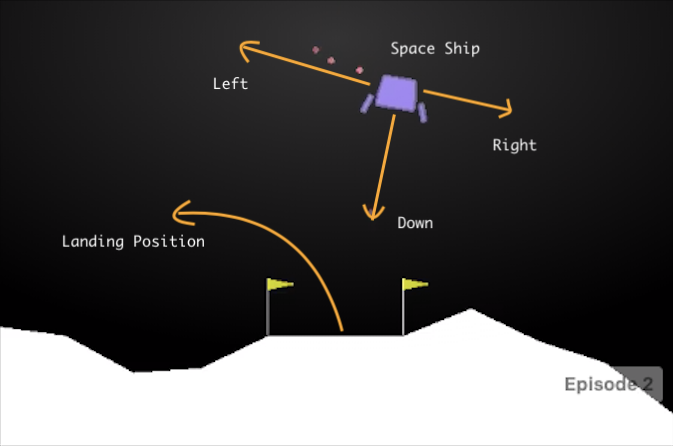
Este es un ejemplo de código detallado:
Paso 1: Instalar las bibliotecas necesarias
1pip install gymnasium gymnasium[box2d] stable-baselines3 torchPaso 2: Importar bibliotecas y entorno de configuración
1import gym
2from stable_baselines3 import DQN
3from stable_baselines3.common.evaluation
4import evaluate_policy
5
6# Create the Lunar Lander environment
7env = gym.make("LunarLander-v2")Paso 3: Definir el modelo DQN
1# Define the DQN model
2model = DQN("MlpPolicy", env, verbose=1)Paso 4: Entrene el modelo DQN
1# Train the model
2model.learn(total_timesteps=100000) # Adjust the timesteps as neededPaso 5: Evaluar el modelo entrenado
1# Evaluate the trained mode
2lmean_reward, std_reward = evaluate_policy(model, env, n_eval_episodes=10)
3print(f"Mean reward: {mean_reward} +/- {std_reward}")
4
5# Optionally, save the model
6model.save("dqn_lunar_lander")Paso 6: Visualizar el modelo entrenado
1import time
2# Load the model if needed
3# model = DQN.load("dqn_lunar_lander")
4# Visualize the model's performanceepisodes = 5
5
6for episode in range(1, episodes + 1):
7 obs = env.reset()
8 done = False
9 score = 0
10 while not done:
11 env.render()
12 action, _states = model.predict(obs)
13 obs, reward, done, info = env.step(action)
14 score += reward
15 print(f"Episode: {episode}, Score: {score}")
16 time.sleep(1)
17env.close()Explicación
- Configuración del entorno: `gym.make («LunarLander-v3") `inicializa el entorno del Lunar Lander.
- Modelo DQN: La clase `DQN` de Stable Baselines3 se usa para definir el modelo con una política MLP.
- Entrenamiento: El método «aprender» entrena el modelo con el número especificado de intervalos de tiempo.
- Evaluación: la función `evaluate_policy` evalúa el rendimiento del modelo en varios episodios.
- Visualización: El bucle renderiza el entorno para visualizar el rendimiento del modelo entrenado en tiempo real.
Consejos adicionales
- Hiperparámetros: es posible que necesite ajustar los hiperparámetros (como la tasa de aprendizaje, el tamaño del lote, etc.) para obtener un mejor rendimiento.
- Punto de control: guarde los modelos intermedios durante el entrenamiento para evitar la pérdida de progreso.
- Monitoreo: usa TensorBoard para monitorear las métricas de entrenamiento en tiempo real.
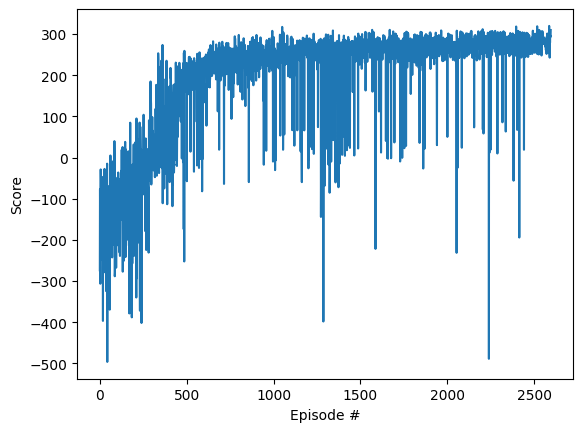
.gif)
Conclusión
DQN es un potente algoritmo de aprendizaje por refuerzo que combina Qlearning y redes neuronales profundas. Al utilizar técnicas como la reproducción de experiencias y las redes de objetivos, DQN aprende de forma eficaz a resolver entornos complejos, como el Lunar Lander de Gymnasium, lo que demuestra su potencial tanto en juegos como en aplicaciones del mundo real. El uso de una red objetivo junto con la red principal garantiza la estabilidad y la coherencia en el aprendizaje, lo que convierte a DQN en un algoritmo sólido y eficiente para una amplia gama de problemas de RL.
Costo y tiempo de ejecución
Esto se entrenó con la GPU T4 de Google Colab Pro
Materiales de aprendizaje adicionales
- Deep Q Learning con DQN: aprendizaje por refuerzo p.5
- La IA aprende a aterrizar un cohete (Lunar Lander) | Aprendizaje por refuerzo
- Documentación del gimnasio - Lunar Lander
- Jugar a Atari con Deep Reinforcement Learning
- Resolver Lunar Lander usando DQN con Keras
- Explicación de Deep Q-Networks
- Grupos miembros de BCS - Deep Q Network DQN
- Udacity - Aprendizaje por refuerzo profundo


